Applications of Trigonometry in Real life: Trigonometry is one of the important branches of mathematics that is concerned with the study of the relationship between the sides and angles of a triangle. The term “trigonometry” is derived from the Greek words trigonon, which means “triangle”, and metron, which means “measure”. The concept of trigonometry is given by the Greek mathematician “Hipparchus”. In ancient times, astronomers used it to find out the distance of the stars and planets from the Earth. Most technologically advanced methods used in Engineering and Physical Sciences today are based on trigonometric concepts.
Trigonometry is classified into two sub-branches:
- Plane trigonometry
- Spherical Trigonometry
Basics of Trigonometry:
There are three basic functions of trigonometry: sine (sin), cosine (cos) and tangent (tan). These three basic functions or ratios are used to derive other important trigonometric functions: cotangent (cot), secant (sec) and cosecant (cosec).
These six trigonometric ratios help establish a relationship between the ratio of sides and the angle of a right-angle triangle. Please find below the details:
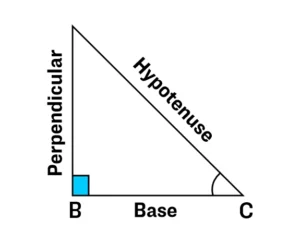
If θ (theta) is the angle in a right-angled triangle formed between the base (BC) and hypotenuse (AC), then
- sin θ = Perpendicular (AB)/Hypotenuse (AC)
- cos θ = Base (BC)/ Hypotenuse (AC)
- tan θ = Perpendicular (AB)/Base (BC)
The value of cot, sec and cosec depends on tan, cot and sin, respectively:
- cot θ = 1/ tan θ = Base (BC)/Perpendicular (AB)
- sec θ = 1/ cos θ = Hypotenuse (AC)/Base (BC)
- cosec θ = 1/sin θ = Hypotenuse (AC)/Perpendicular (AB)
Real-Life Applications of Trigonometry:
The applications of trigonometry are seen in different fields in real life. Let us have a look at all these fields to understand the application of trigonometry:
1. Trigonometry in Measuring Heights:
Trigonometry is used in measuring the height of building, mountain, tree, etc. The height of a building or a mountain can easily be determined by measuring the horizontal distance from the base and the angle of elevation to the top.
Let us take an example to understand the concept:
A boy is standing near a building and wonders, “What is the height of the building?” Using trigonometric formulas, the height can be calculated if the distance between the building and the boy and the angle formed when the building is viewed from the ground are given.
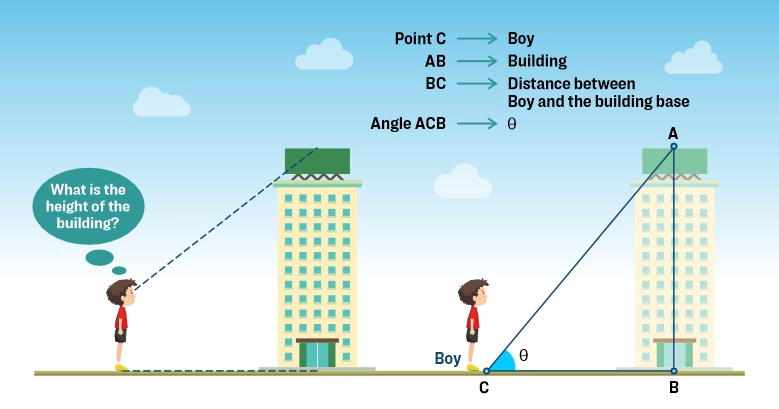
Let’s say the angle of elevation is θ, then:
tan θ = Height/Distance between boy & building
Distance = Height/ tan θ
Let us assume that the distance is 30m and the angle formed is 45°, then
Height = 30/tan 45°
Since, tan 45° = 1
then, Height = 30 m
2. Trigonometry in Astronomy:
- The solar system has fascinated the human beings across the world since the start of the civilisation.
- Astronomers use trigonometry to calculate the distance between the stars, planets & other bodies present in the solar system from Earth.
- NASA scientists also use this mathematical technique to design and launch space shuttles and rockets.
- Without the knowledge of trigonometry, there would not be any satellites in orbit or missions to the moon by humans.
3. Trigonometry in Flight Engineering:
- Trigonometry is used to calculate the direction, speed, and slope of the aeroplane’s path from landing to take-off.
- It is used to determine the ideal take-off and landing angles and speeds, even when the winds are blowing.
- The wind plays an important role in calculating the angle at which the flight will land and take off and the best speed for that aeroplane.
| Are you facing anxiety with your subject? Check out these helpful blogs: |
|
|
4. Trigonometry in Navigation:
- The use of trigonometry is also seen in navigating directions with the help of a compass that provides a straight direction to the destination.
- Trigonometry is also employed to calculate the distance between a location in the sea and the shore.
- Also, the satellite navigation system uses trigonometric functions such as the law of cosine to calculate simple equations to help in locating the satellites in the Earth’s orbit.
5. Trigonometry in Construction:
- In construction sites, trigonometry is used in measuring the ground surface and fields.
- During building construction, aspects like roof inclination, rook slopes, perpendicular and parallel walls, light angles, shun shading, etc., require trigonometry.
- Trigonometry also helps while installing the ceramic tiles and stones during construction.
6. Trigonometry in Marine Biology:
Marine biologists study marine life, including plants, animals, and other species that are present inside the ocean.
- Trigonometry is used in marine biology to predict the distance and at what angle a creature or a plant is from the scientist.
- The angle might be a depression angle or an elevation angle, depending on the observer’s location. The water level is considered the right-angled triangle’s base, while the object’s depth is considered to be the height slant distance.
- Using the trigonometric function, marine biologists evaluate the size of large animals and understand their behaviour.
7. Other Uses of Trigonometry:
There are so many other trigonometry uses also, which are mentioned below:
- Trigonometry is also used in criminology or crime scenes to determine the estimated cause of a collision in an accident or at what angle a gunshot was.
- The trigonometric functions (sine and cosine) help in describing sound and light waves.
- Oceanography also uses trigonometry to measure the height of waves and tides.
- Trigonometry is also used in cartography (creation of maps) and in the naval and aviation industries.
- Marine biologists use trigonometry to determine the deepness of sunlight and its impact on algae’s photosynthesis.
If you find and/or can relate Applications of Trigonometry to your daily life, please share your experience in the comment box. It will help others understand this easily.
For such more content, stay connected with us!
Read More. . . .




