- Call Us :
- Mail Us :
- Request a Call



Mathematics can be daunting for students, but with the right approach and practice, students can score well in the subject. Students preparing for the class 10 board exams often encounter difficulties and seek solutions to master the subject. In this blog, we have included the 10 Most Challenging Class 10th Math Problems which students commonly face and will share tips and strategies to solve these complex problems. In this blog, we have covered some major problems faced by the students during the preparation and the preparation strategy they can follow.
The difficulty level of the problems may vary depending on the student’s understanding and learning style. Still, there are some specific problems that students face difficulty while solving. Below, we have listed some of these maths problems with tips to solve them:
Solving trigonometry-related problems requires an in-depth understanding of trigonometry concepts, trigonometric identities, and algebraic manipulations.
Example: Prove that cos²A + sin²A = 1.
Proof: Let us take a right-angled triangle ABC, having a right angle at B, we have:
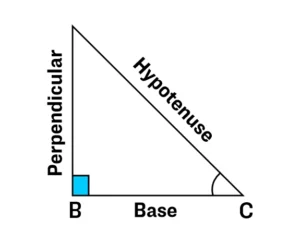
AB² + BC² = AC² –(1)
Dividing the eq (1)by AC², we get
AB²/AC² + BC²/AC² = AC²/AC²
i.e. (AB/AC)² + (BC/AC)² = (AC/AC)²
(cos A)² + (sin A)² = 1
i.e. cos² A + sin² A = 1
Also Read: Real-Life Applications of Trigonometry
Sometimes, it may be difficult for students to solve and decode real-world problems into quadratic equations.
Example: A rectangular garden has an area of 120 square meters. If its length is 5 meters more than its width, find the dimensions of the garden.
Solutions: Let us assume that the width of the garden is x, then the length will be (x + 5)
We know that the area of a rectangular garden is:
area = length * width
120 = (x + 5) * x
120 = x² + 5x
x² + 5x – 120 = 0
Solving the above equation using factorisation:
(x + 15x)(x – 8x) = 0
x = -15 or 8
Since, the width of the garden cannot be negative, therefore width (x) = 8 meters
Length = (x + 5) = (8 + 5) = 13 meters
Proving theorems and solving problems related to geometrical shapes may be difficult sometimes as they involve complex logical reasoning.
Example: Prove that the angle in a semicircle is a right angle.
Proof: Let us understand by the figure:

In the above figure, AOB is a straight line passing through the centre O.
Therefore, angle subtended by arc AB at O is ∠AOB = 180°
According to the theorem, the angle subtended by an arc at the centre is doubled the angle subtended by it on any point on the remaining part of the circle.
∠AOB = 2∠APB
∠AOB/2 = ∠APB
180°/2 = ∠APB
∠APB = 90°
Hence proved
It may be difficult for the students to calculate the surface area and volume of different complex shapes can be challenging.
Example: Find the total surface area of a cone with radius 5 cm and height 12 cm.
Solution:
Surface area of a cone = πr(r + l)
where r is the radius and l is the slant height.
Slant height (l) = √(r² + h²)
l = √(5² + 12²) = 13 cm
Surface area = π * 5 * (5 + 13) = 282.74 cm²
| Check out our few helpful blogs: |
Understanding concepts like mean, median, mode, and probability can be difficult. Sometimes, students face difficulty while solving problems involving data interpretation.
Simplifying expressions with exponents, radicals, and factoring can sometimes be complex for the students.
Example: Simplify the expression (2x²y³)^4 / (4x³y)^2.
Solution:
= (16x^8y^12) / (16x^6y^2)
= x^(8-6) * y^(12-2)
= x²y¹⁰
Solving multiple equations simultaneously can be confusing for the students due to the complex nature of the questions.
Visualising & applying formulas can sometimes be difficult for the students. Coordinate geometry problems involve finding equations for lines, circles, and other geometric figures.
Understanding and applying the rules of exponents and radicals involving simplification and rationalisation can be challenging.
Identifying and solving proportions involving direct and inverse variation can be tricky for the students sometimes.
The above are some problems that students face while preparing for the Class 10 exams. These are some general problems, there might be some other problems too that as a student you can face during the preparation, if there is so you can drop your problems in the comment box and we will try to solve and help you out in this.
Our Support
Copyright © 2025 Allen Overseas. All Rights Reserved.